Statistik selalu digunakan ketika parameter yang menggambarkan karakteristik populasi tidak diketahui. Statistik  akan mengambil sebagian (kecil) dari populasi untuk dilakukan pengukuran, kemudian hasil pengukuran tersebut dijadikan sebagai kesimpulan ikterhadap keseluruhan populasi. Sebagian (kecil) dari populasi tersebut dinamakan sampel. Ibarat kita ingin mengetahui rasa sepanci sayur asem, kita tidak perlu menenggak satu panci tapi cukup mencicipinya sebanyak satu sendok.

Terdapat dua jenis statistik yang digunakan ketika penelitian, yaitu:

  1. Statistik deskriptif  (descriptive statistics), yang hanya menggambarkan data atau seperti apa data ditunjukkan.
  2. Statistik inferensi (inferential statistics), yang mencoba untuk mencapai  kesimpulan (bersifat induktif) dari data dengan kondisi yang lebih umum (Trochim, 2006), misal: point estimation, confidence interval estimation, hypothesis testing.

Definisi lengkap statistik deskriptif adalah metode-metode yang berkaitan dengan pengumpulan dan penyajian suatu gugus data sehingga menaksir kualitas data berupa jenis variabel, ringkasan statistik (mean, median, modus, standar deviasi, etc), distribusi, dan representasi bergambar (grafik), tanpa  rumus probabilistik  apapun (Walpole, 1993; Correa-Prisant, 2000; Dodge, 2006).

Di SPSS, analisis statistik deskriptif dilakukan dengan mengklik menu [Analyze] -> [Descriptive Statistics], kemudian akan muncul beberapa pilihan seperti Frequencies, Descriptives, Explore, Crosstabs, etc. Dalam berbagai penelitian, perintah-perintah ini sering diabaikan karena beberapa fungsi analisis lain sudah otomatis menyertakan analisis deskriptif.

Fitur Frequencies sudah pernah kita coba pada saat praktik entri data dalam postingan berjudul: “SPSS Data Entry: Panduan Input, Transformasi, dan Analisis Data“. Dengan menggunakan contoh dataset dari postingan tersebut, kita akan mempraktikkan operasi pada submenu Descriptives, Explore, dan Crosstabs.

A. Descriptives

Dengan menggunakan contoh dataset postingan sebelumnya, langkah-langkah perintah Descriptives adalah sebagai berikut:

(1) Klik menu [Analyze] -> [Descriptives Statistics] -> [Descriptives], muncul dialog box Descriptives.

(2) Masukkan variabel yang akan dianalisis ke form Variables(s).

(3) Klik [Options] untuk melakukan setting optional, muncul dialog box Descriptives: Options.

(4) Centang analisis yang diperlukan, saya memilih:

  • Mean
  • Std. deviation
  • Minimum
  • Maximum
  • Kurtosis
  • Skewness

(5) Centang Variable list pada form Display Order.

 

spss-desc-9

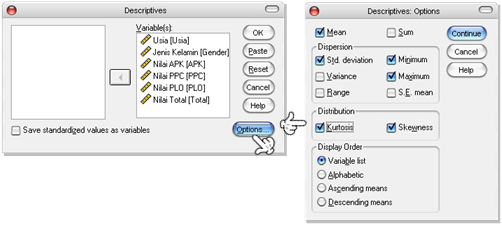
Gambar 1. Langkah-Langkah Descriptives Statistics

 

(6)  Klik [Continue] dan [OK]. Hasil analisis akan terlihat seperti tabel yang ditunjukkan Gambar 2 di bawah ini:

 

spss-desc-10

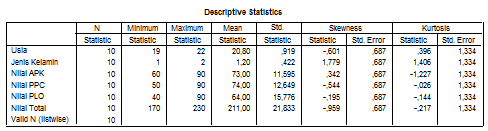
Gambar 2. Output Descriptives

 

Tabel output di atas menunjukkan jumlah pengukuran (N), nilai minimum (Minimum), nilai maksimum (Maximum), nilai rata-rata (Mean), standar deviasi (Std.), Skewness, dan Kurtosis dari masing-masing variabel.

Nilai skewness merupakan ukuran kesimetrisan histogram, sedangkan kurtosis merupakan ukuran datar atau runcingnya histogram. Idealnya nilai skewness dan kurtosis pada distribusi normal adalah nol. Oleh karena itu:

  • Jika nilai skewness positif maka distribusi data “miring ke kiri distribusi normal” (ada frekuensi nilai yang tinggi di sebelah kiri titik tengah distribusi normal), sebaliknya apabila skewness negatif maka distribusi data ”miring ke kanan distribusi normal” (kiri bagi kita yang melihatnya).
  • Jika nilai kurtosis positif maka distribusi data “meruncing” (ada satu nilai yang mendominasi), sebaliknya apabila Kurtosis Negatif maka distribusi data “melandai” (varians besar).

Perhatikan Gambar 2 di atas, variabel Usia memiliki skewness negatif dan kurtosis positif, artinya distribusinya “miring ke kiri distribusi normal” dan “meruncing”.

Pada variabel nilai APK, nilai skewness positif dan nilai kurtosis negatif, artinya distribusinya “miring ke kanan distribusi normal” dan “melandai”. Sebagai pembuktian, buat histogram untuk variabel Usia dan Nilai APK. Berikut caranya:

  • Klik menu [Graphs] -> [Histogram], maka muncul dialog box Histogram.
  • Pilih variabel Usia dan masukkan dalam form Variable.
  • Centang Display normal curve, untuk memperlihatkan kurva normal.
  • Selanjutnya klik [OK].

Lakukan langkah yang sama untuk variabel nilai APK. Hasilnya bisa dilihat pada Gambar 4.

 

spss-desc-11

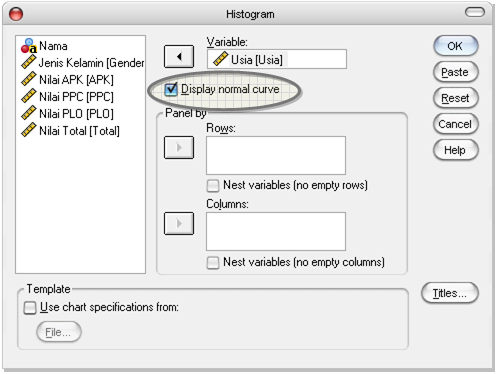
Gambar 3. Menampilkan Histogram bersama Kurva Normal

 

spss-desc-12

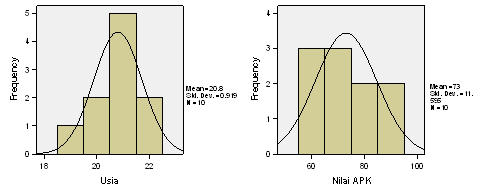
Gambar 4. Analisis Skewness dan Kurtosis pada Histogram

 

Gambar 4 di atas menunjukkan histogram untuk variabel Usia  memiliki distribusi “miring ke kiri distribusi normal” karena nilainya skewness negatif  dan “meruncing” karena nilai kurtosis positif.

Sebaliknya, histogram untuk variabel Nilai APK  memiliki distribusi “miring ke kanan distribusi normal” karena nilainya skewness positif  dan “melandai” karena nilai kurtosis negatif.

Di sini, anda bisa menentukan apakah distribusi tersebut normal atau tidak. Anda bisa saja menyatakan normal, karena menyerupai bentuk lonceng tetapi agak serong, tapi  orang lain mungkin akan menyatakan tidak normal karena jauh dari bentuk lonceng. Jika sulit mengambil keputusan, silahkan lakukan pengujian normalitas yang lebih advance, misal dengan Uji Kolmogorov-Smirnov. Selanjutnya, kita masuk pada penggunaan perintah Explore.

 

B. Explore

Perintah Explore digunakan untuk membandingkan antara dua atau lebih kelompok dengan satu  variabel. Sebagai contoh, jika kita menggunakan Jenis Kelamin sebagai variabel independen; variabel ini mendefinisikan kelompok (Laki-Laki dan Perempuan), kemudian membandingkannya dengan variabel lain, seperti Usia. Perintah Explore; contoh  dalam kasus mean, akan menghasilkan  berapa rata-rata usia laki-laki dan berapa rata-rata usia perempuan.  Ukuran-ukuran yang dihasilkan perintah Explore  antara lain: ukuran-ukuran pemusatan data (mean dan median), ukuran penyebaran (range, interquartile range, standar deviasi, varians, minimum, dan maksimum), ukuran kurtosis, dan skewness.

Berikut langkah-langkah perintah Explore:

(1) Klik menu [Analyze] -> [Descriptives Statistics] -> [Explore], muncul dialog box Explore.

(2) Isi variabel Jenis Kelamin pad form Factor List.

(3) Isi variabel Usia, Nilai APK, Nilai PPC, Nilai PLO, dan Nilai Total pada form Dependent List.

(4) Pada  form Display ada tiga pilihan:

  • Klik [Plots] bila perlu grafik boxplot.
  • Klik [Statistics] bila tidak perlu grafik boxplot.
  • Klik [Both] bila perlu keduanya.

(5)  Terakhir klik [OK].

 

spss-desc-13

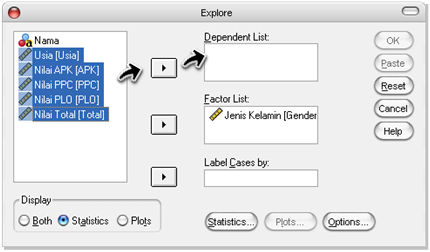
Gambar 5. Dialog Box Explore

 

spss-desc-14

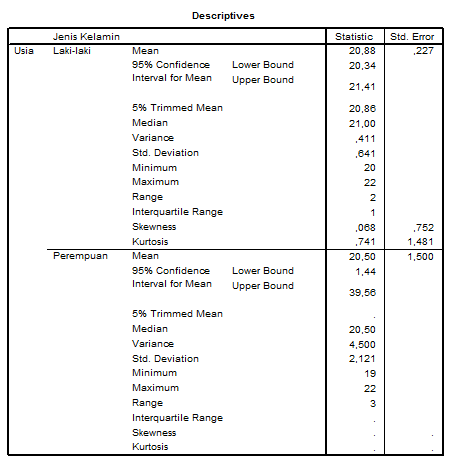
Gambar 6. Contoh Output Explore untuk Variabel Usia

 

Selanjutnya, kita masuk pada penggunaan perintah Crosstabs.

 

C. Crosstabs

Jika perintah Frequencies digunakan untuk memperoleh jumlah pada nilai-nilai sebuah variabel tunggal, perintah  Crosstabs digunakan untuk memperoleh jumlah pada nilai-nilai lebih dari satu variabel. Apabila analisis statistik deskriptif sebelumnya mengolah data secara keseluruhan dalam setiap variabel dengan menghitung perhitungan statistik seperti Mean, Standar deviasi, Kurtosis, etc. Pada Crosstabs, setiap nilai pada variabel yang dianalisis dijabarkan jumlahnya, dengan begitu kita dapat mengetahui berapa jumlah subyek laki-laki yang berusia 19 tahun, 20 tahun, dst. Deskripsi data pada Crosstabs akan disajikan dalam bentuk tabel silang (crosstab) yang terdiri dari baris dan kolom.

Berikut langkah-langkah perintah Crosstabs:

(1)  Klik menu [Analyze] -> [Descriptives Statistics] -> [Crosstabs], muncul dialog box Crosstabs.

(2) Isi variabel Jenis Kelamin pada form Row(s).

(3) Isi variabel yang akan dianalisis, contoh variabel Usia pada form Column(s).

 

spss-desc-15

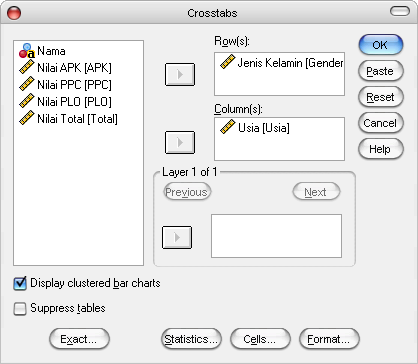
Gambar 7. Dialog Box Crosstabs

 

(4)  Centang [Display clustered bar charts] untuk menampilkan chart bar dari output.

(5) Untuk dialog box [Statistics], [Cells], dan [Format] biarkan sesuai dengan default SPSS.

(6)  Terakhir klik [OK].

 

spss-desc-16

Gambar 8. Output Crosstabs

 

spss-desc-17

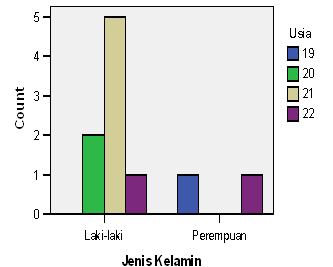
Gambar 9. Clustered Bar Charts

 

Statistik deskriptif memberikan informasi inti dari kumpulan data, seperti ukuran-ukuran pemusatan data (mean dan median), ukuran penyebaran (range, interquartile range, standar deviasi, varians, minimum, dan maksimum), ukuran kurtosis, dan skewness serta representasi piktorialnya. Tabel, diagram, dan grafik yang sering ditemukan di majalah dan koran-koran merupakan salah satu contoh penggunaan statistik deskriptif.

 

 

Rujukan:

Correa-Prisant, M. (2000). Descriptive statistics. Retrieved from http://www.pitt.edu/~super1/lecture/lec0421/index.htm

Dodge, Y. (2006). The Oxford dictionary of statistical terms (p. 111). New York: Oxford University Press.

Patria, B. (2007, August 17). Entry Data: Seri Tutorial SPSS 03. Retrieved from http://inparametric.com/bhinablog/download/03_entri_data.pdf

__________. (2007, August 17). Analisis Deskriptif: Seri Tutorial SPSS 04. Retrieved from http://inparametric.com/bhinablog/download/04_analisis_deskriptif.pdf

SPSS. (2005). SPSS (Version 14.0) [Computer software]. Chicago-Illinois: SPSS, Inc.

Trochim, W. M. K. (2006). Descriptive statistics. Research Methods Knowledge Base. Retrieved from http://www.socialresearchmethods.net/kb/statdesc.php

Walpole, R. E. (1993). Pengantar statistika. Jakarta : PT Gramedia Pustaka Utama.

Unknown's avatar

Published by Eris Kusnadi

17 thoughts on “ SPSS untuk Statistik Deskriptif: Panduan Belajar dari Nol ”

  6. halo pak, saya riama.
    saya mau nanya pak.
    saya melakukan uji F dengan y=produktivitas, x1=umur, x2=pengalaman
    kerja dan x3=pendidikan terakhir.
    nah, nilai signifikan uji F (yg ditabel anova) itu= . (cuma titik aja
    pak) dan R-square nya itu 100, serta nilai-nilai residualnya 0
    semua… itu bagaimana ya pak menjelaskannya.
    terimakasih pak untuk kesediaan membagi ilmunya 🙂

    Like

    Reply

  8. siang pak, saya mau tanya arti std.devisiasi dalam uji statistik deskriptif itu untuk apa ya ? soalnya saya masih kurang paham guna nya standar devisiasi. thx

    Like

    Reply

  11. Mas. Jika kita melakukakan olah data kuesioner. Lalu nilai minimum dan maximum itu nilai apa ya mas? Bagaimana maksud nilai tsb ya? Terimakasih.

    Like

    Reply

  12. 1. ANOVA
    #ANOVA
    #Input Data
    X = read.table(“nama file.txt”, header = TRUE);
    #Bentuk data menjadi sebuah vektor
    X = c(t(as.matrix(x))) #Vektor Data
    #Definisikan variabel baru untuk perlakuan dan banyak pengamatan
    F = c(“Variabel 1”,…,”Variabel n”) #faktor variabel perlakuan
    K #banyak jenis perlakuan
    N #banyak pengamatan per perlakuan
    M #banyak seluruh pengamatan

    #Buat vektor faktor perlakuan sesuai dengan vektor r
    Tm = gl(k, l, n*k, factor(f)) #vektor perlakuan

    #Function
    Av = aov(r ~ tm)
    summary (av) #tabel ANOVA
    #F critical atau tabel
    Df1 = k – 1
    Df2 = N – k
    Alpha = 0.05
    Fcrit = qf(1-alpha,df1,df2)
    #hasil : bandingkan Pvalue bandingkan dengan alpha atau bandingkan F hitung dengan F tabel
     

    #Contoh
    #Input Data
    X = read.table(“D:/Statistik/R/Rmodul/Hormone.txt”, header = TRUE);
    X #Bentuk data menjadi sebuah vektor
    R = c(t(as.matrix(x))) #Vektor Data

    #Variabel perlakuan
    F = c(“Au”, “Si”, “Gi”)
    K = 3
    N = 5
    M = 15

    #Vektor Perlakuan
    Tm = gl(k, l, n*k, factor(f))

    #Function
    Av = aov(r ~ tm)
    Summary(av) #tabel ANOVA

    #F critical atau tabel
    Df1 = k – 1
    Df2 = N – k
    Alpha = 0.05
    Fcrit = qf(1-alpha, df1, df2)
    Fcrit
     
    #ANOVA DWI FACTOR
    #Input Data
    X = read.table(“nama file.txt”, header = TRUE);
    #Bentuk Data menjadi sebuah vektor
    R = c(t(as.matrix(x))) #Vektor Data

    #Definisikan variabel baru untuk perlakuan dan banyak pengamatan
    F1 = c(“variabel 1”, … , “variabel n”) #faktor perlakuan pertama
    F2 = c(“faktor 1”, … , “faktor n”) #faktor perlakuan kedua
    K1 = length(f1) #banyak jenis perlakuan pertama
    K2 = length(f2) #banyak jenis perlakuan kedua
    N #banyak pengamatan per perlakuan
    M #banyak seluruh pengamatan

    #Buat vektor faktor perlakuan sesuai dengan vektor r
    Tm1 = gl(k1, 1, n*k1*k2, factor(f1)) #vektor perlakuan pertama
    Tm2 = gl(k2, n*k1, n*k1*k2, factor(f2)) #vektor perlakuan kedua

    #Function
    Av = aov(r ~ tm1*tm2) #interaksi
    Summary(av) #tabel ANOVA

    #hasil : bandingkan Pvalue bandingkan dengan alpha
     
    #CONTOH
    #Input Data
    Df3 = read.csv(“D:/Statistik/R/Rmodul/Rudal.csv”)
    R = c(t(as.matrix(df3)))
    F1 = c(“b1”, “b2”, “b3”, “b4”)
    F2 = c(“a1”, “a2”, “a3”)
    K1 = length(f1)
    K2 = length(f2)
    N = 2

    #vektor perlakuan
    Bahanbakar = gl(k1, 1, n*k1*k2, factor(f1))
    Rudal = gl(k2, n*k1, n*k1*k2, factor(f2))

    #tabel ANOVA Dwi Faktor
    Av = aov(r ~ bahanbakar * rudal)
    Summary(av)
     
    #CONTOH
    #Input Data
    Df3 = read.csv(“D:/Statistik/R/Rmodul/Rudal.csv”)
    R = c(t(as.matrix(df3)))
    F1 = c(“b1”, “b2”, “b3”, “b4”)
    F2 = c(“a1”, “a2”, “a3”)
    K1 = length(f1)
    K2 = length(f2)

    #Vektor perlakuan
    Bahanbakar = gl(k1, 1, n*k1*k2, factor(f1))
    Rudal = gl(k2, n*k1, n*k1*k2, factor(f2))
    #tabel ANOVA Dwi Factor
    Av = aov(r ~ bahanbakar*rudal)
    Summary(av)
     
    #Regresi Linear
    #Input
    Data = read.table(“nama file.txt”, header = TRUE)
    X #variabel bebas
    Y #variabel terikat
    #scatterplot untuk x dan y
    Plot(x,y)
    #korelasi dan kovariansi
    Cor(x,y)
    Cov(x,y)

    #Koefisien Model
    Model = lm(y ~ x)
    Summary(model) #Informasi yang didapat adalah
    #koefisien model, p-value koefisien, r-square
    #Plot Model
    Abline(model)
    #Residual
    Model.res = resid(model)
    Plot(x, model.res, ylab=”y”, xlab = “x”, main = “Plot Residual”)

    #Kenormalan Residual
    Model.stdres = rstandard(model)

    #Plot Kenormalan Residual
    Qqnorm(model.stdres, ylab = “Standarized Residuals”, xlab = “Normal Scores”, main = “Plot Kenormalan Residual”)
     
    #Input
    Biayaiklan = read.table(“D:/Statistik/R/Rmodul/Biayaiklan.txt”, header = TRUE)
    Attach(Biayaiklan)

    #Scatterplot
    Plot(biaya,penjualan)
    #Correlation and covariance
    Cor(biaya, penjualan)
    Cov(biaya, penjualan)
    #Koefisien model
    #x : biaya, y : penjualan
    Model = lm(penjualan ~ biaya)
    Summary(Model)
    #Plot model
    Abline(Model)
    #Residual
    Model.res = resid(model)
    Plot(biaya, model.res, ylab = “Residual”, xlab = “Biaya Iklan”, main = “Plot Residual Biaya Iklan”)

    #Kenormalan Residual
    Model.stdres = rstandard(model)

    #Plot Kenormalan Residual
    Qqnorm(model.stdres, ylab = “Standarized Residuals”, xlab = “Normal Scores”, main = “Plot Kenormalan Residual”)
     
    #PERIKSA PENCILAN PADA RESIDU
    #Residual
    Model.res = resid(model)
    Plot(biaya, model.res, ylab = “Residual”, xlab = “Biaya Iklan”, main = “Plot Residual Biaya Iklan”)
     
    #Regresi Logistik
    #Contoh 1
    #Input
    Mydata  read.csv(“D:/Statistik/R/Rmodul/Pembelian.csv”)
    Head(mydata)
    #dependent variable : pembelian
    #independent variable : umur, pendapatan (1 : low, 2 : medium, 3 : high), #status (0 : single, 1 : married)

    #using logit model
    Mydata$pendapatan < — factor (Mydata$pendapatan)
    Mydata$status < — factor(Mydata$status)
    Mylogit <– glm(pembelian ~ umur + pendapatan + status, data = mydata, family = “binomial”)
    Summary(mylogit)
     
    #REGRESI MULTIVARIAT
    #Input
    Mydata <– read.csv(“D:/Statistik/R/Rmodul/Permintaan.csv”, head = TRUE)
    Mydata
    #independent variable : harga, pendapatan
    #dependent variable : permintaan
    Model <– lm(Permintaan ~ Harga + Pendapatan, data = mydata)
    Summary(model, corr = TRUE)

    #Residual
    Model.res = resid(model)
    Plot(mydata$Harga,model.res, ylab = “Residual”, xlab = “Harga”, main = “Plot Residual Harga”)
    plot (mydata$Pendapatan, model.res, ylab = “Residual”, xlab = “Pendapatan”, main = “Plot Residual Pendapatan”)

    #Kenormalan Residual
    Model.stdres = rstandard(model)

    #Plot Kenormalan Residual
    Qqnorm(model.stdres, ylab = “Standarized Residuals”, xlab = “Normal Scores”, main = “Plot Kenormalan Residual”)
    Qqline (model.stdres)
     

    Like

    Reply
  16. Pingback: Analisis Deskriptif: Pengertian, Metode, dan Cara Membuatnya
  17. Pingback: SPSS dalam Proses Entri Data – Blog Eris

Leave a reply to awaluddin Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.